函數4：$f(x) = \frac{1}{x}$

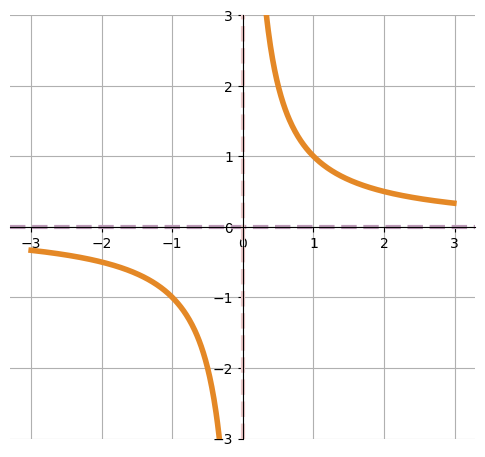
在畫函數圖形前，可以先用紙筆大致看一下函數長什麼樣子，例如：漸進線、critical point 等。之後，使用 Python 畫圖時才比較不容易畫錯，錯過函數細節。函數圖形如下，特點為有兩條漸進線：x=0 與 y=0。在畫這兩條水平與垂直漸進線時，比較簡便的做法為直接給兩點畫一條直線。例如：

1. plt.plot([0, -10], [0, 10], linestyle='-', color='black') 在點 (0, -10) 到點 (0, 10) 之間畫直線。
2. 或用 x = np.arange(0, 1, 0.01) 設置要畫的線 X 的範圍，再以 asyp_1 = [_in_x] 設置要在 X 軸哪點至哪點繪線，最後使用 plt.plot(x, asymp_1, linestyle='-', color='black) 畫出來。
3. 或若為水平或垂直線，也可以直接使用 plt.axhline 、 plt.axvline。

畫此函數的重點在於：因為函數在 x=0 時沒有值，所以須分為 x>0 或 x<0 兩段畫圖。為了凸顯此函數的對稱性，將圖片設定為正方形來輸出，並去除邊框，把網格長寬設為相同比例。

# function 4: f(x) = 1/x

xmin, xmax = -3, 3
ymin, ymax = -3, 3

x1 = np.arange(0, xmax, 0.01)
x2 = np.arange(xmin, 0, 0.01)

def f(x): return 1/x

# 畫圖
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=[6, 6]) # 圖片比例
plt.plot(x1, f(x1), color='#e48826', linewidth=4)
plt.plot(x2, f(x2), color='#e48826', linewidth=4)

# 漸進線
plt.axhline(y=0, color='#bb99b7', linewidth=3, linestyle='--')
plt.axvline(x=0, color='#ecc8c9', linewidth=3, linestyle='--')

plt.xticks(np.arange(xmin, xmax+0.5, 1))
plt.ylim([ymin, ymax])
plt.yticks(np.arange(ymin, ymax+0.5, 1))
plt.grid(True)

# 去除邊框
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_position(('data', 0))
ax.spines['bottom'].set_position(('data', 0))
ax.set_aspect(1) # 網格長寬比例為相同

plt.show()

函數5：$f(x) =\frac{1}{2\sqrt{2\pi}}e^{-\frac{(x-1)^2}{8}}$

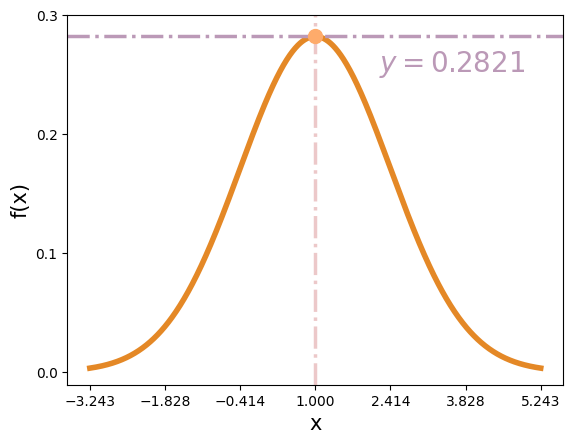
函數圖形如下，對稱於 x=\mu=1，\sigma^2=2。Python 程式碼如下，因為撰寫自並函數過程複雜，為避免發生錯誤，直接使用特殊函數指令。以 mu, sigma = 1, np.sqrt(2) 先設置含函數之參數，再用 xlim = [mu - 3 * sigma, mu + 3 * sigma] 與 x = np.linspace(xlim[0], xlim[1], 1000) 利用向量的手段設定 x 的範圍，然後用 y = norm.pdf(x, mu, sigma) 特殊函數指令，計算 y 值，即函數值。最後將塗瑱指令存到 plt.plot(x, y)。除使用上述的特殊函數指令之外，也可以考慮使用 SciPy 函數庫中的特殊函數。

# function 5: f(x) = 1/(2*2^(1/2)*pi)*exp^{-(x-1)^2/8}
# Normal PDF with (mu, sigma) = (1, 2^(1/2))

from scipy.stats import norm 

mu, sigma = 1, 2**(1/2)
xlim = [mu - 3 * sigma, mu + 3 * sigma] # x 的範圍
x = np.linspace(xlim[0], xlim[1], 1000) 
y = norm.pdf(x, mu, sigma) # y 的範圍

plt.plot(x, y, color='#e48826', linewidth=4) # 畫函數
plt.axvline(x=mu, linestyle='-.', linewidth=2.5, color='#ecc8c9') # 垂直線
plt.axhline(y=y.max(), linestyle='-.', linewidth=2.5, color='#bb99b7') # 水平線
plt.plot(mu, y.max(), 'o', color='#feab6b', markersize=10)
plt.text(mu + 1.2, y.max() - 0.03, '$y=0.2821$', fontsize=20, color='#bb99b7')

plt.xlabel('x', fontsize=15), plt.ylabel('f(x)', fontsize=15)
plt.xticks(np.arange(xlim[0], xlim[1]+1, sigma), fontsize=10)
plt.yticks(np.arange(0, 0.4, 0.1), fontsize=10)
# plt.grid(True)
plt.show()

函數6：$f(x) = \sqrt[3]{x^2}$

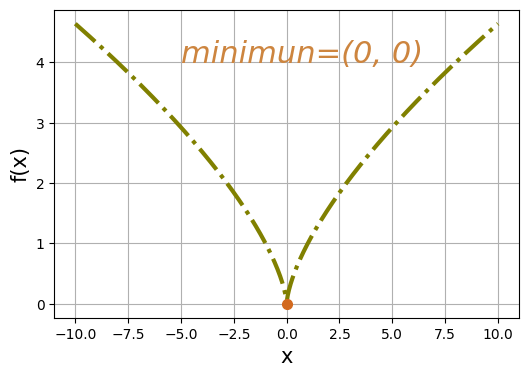
函數圖形如下，對稱於 x=0，其在原點有最小值 0。特別注意的是

1. 函數 6 由一階微分為 0 求解得知：其在 x=0 時有一個 critical point，此在作圖前應注意。
2. 圖片中的說明文字不僅可以調整顏色與文字大小，還可以更換字體。例如：此處使用 ax.text(*) 中設置字體為 style='italic' ，或使用fontstyle='italic'也可以。

# function 6: f(x) = (x^2)^(1/3)

xmin, xmax = -10, 10
x = np.linspace(xmin, xmax, 1000)

def f(x): return np.power((x**2), 1/3) # 目標函數

fig = plt.figure(figsize=[6, 4]) # 把作圖的指令存在 fig

# use axis object
ax = plt.gca() # get current axis
ax.plot(x, f(x), color='olive', linewidth=3, linestyle='-.')
ax.set_xlabel('x', fontsize=15), ax.set_ylabel('f(x)', fontsize=15)
ax.text(-5, 4, 'minimun=(0, 0)', color='peru', fontsize=22, style='italic')
plt.plot(0, 0, 'o', color='chocolate', markersize=7)

ax.grid(True)
plt.show()

下一篇的做圖內容會更有挑戰，作圖前需要注意更多的函數 critical points ，才可以將函數完整的表現出來。